
Cube volume and surface area calculator will help students immensely as we have also put certain examples and solution to understand the math behind it.But before you know about the volume and surface are calculation, will it not be good that you understand why you must know the math of computing volume and surface area of cube?
Real life use of cube volume and surface area calculation
Here are a few real-life examples where you might need to compute the volume or surface area of a cube:
- Packaging: If you work in the packaging industry, knowing math of volume & surface area of cube will help you decide how many items you can fit in the box, or how much packing material you’ll need to fill the box.
- Construction: Architects and builders often need to calculate the surface area of a cube-shaped building to determine how much paint or other finishing materials they’ll need. They might also need to calculate the volume of a cube-shaped room to determine how much flooring or insulation will be required.
- Gardening: If you’re a gardener, you might need to calculate the volume of a cube-shaped container to determine how much soil or compost you’ll need to fill it. You might also need to calculate the surface area of a cube-shaped garden bed to determine how much mulch you’ll need to cover it.
- Cooking: In cooking, measuring ingredients is crucial for accuracy. For example, you might need to calculate the volume of a cube-shaped container to determine how much flour or sugar it can hold.
- Shipping: Shipping companies use the volume of packages to determine shipping rates. If you’re sending a cube-shaped package, you’ll need to calculate its volume to determine how much it will cost to ship.
Cube Volume and Surface Area Calculator
What is a Cube?
A cube or a regular hexahedron (hexa means six) is a closed space having six identical square faces joined along their edges. Three edges join at each corner to form a vertex.
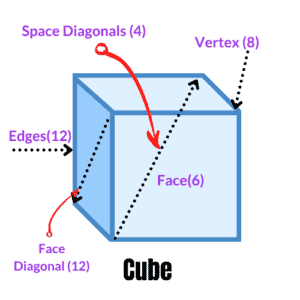
| It has 6 sides or faces which are all squares |
| It has 12 equal length edges. |
| It has 8 vertices or points where 3 edges meet. |
| Each face of a cube has two diagonals. Thus, it has a total of 12 face diagonals. |
| Space diagonals are line segments linking the opposite corners of a cube. A cube has 4 space diagonals. |
Cube Surface Area Formula
The surface area of cube is the sum of areas of all the faces of the cube, that covers it. The formula for the surface area of a cube is equal to six times of square of the length of the sides of the cube.
Surface area of cube= 6s2 Square Unit where s represents a side of the cube
What is Cube Volume Formula?
A cube has all edges the same length. Therefore, the volume of a cube is determined by multiplying the length of any edge three times i.e SxSxS where s is the length of the edge. Or as a formula: volume = S3
What is Cube Face Diagonal Formula?
The line segments linking the opposite corners of a faceis called face diagonals. There are 12 face diagonals in a cube.The length of the face diagonals is given by the formula face diagonal=√2S2
What is the Cube Surface Diagonal Formula?
The line segments linking the opposite corners of a cube,passing through its interior. A cube has 4 space diagonals. The formula for length space diagonal=√3S2 where s is the length of one side (edge).
Calculating Cube Surface Area
Calculating the surface area and volume of a cube is relatively straightforward. Here’s a step-by-step tutorial on how to do it.
How to Calculate Surface Area of Cube?
The surface area of cube is the sum of the areas of all six faces of the cube.
Formula: SA = 6s^2, where s is the length of one side of the cube.
Steps:
- Measure the length of one side of the cube (in any unit of measurement).
- Square the length of one side (multiply it by itself).
- Multiply the result by 6 to get the total surface area of the cube.
Example:
Suppose the length of one side of the cube is 4 cm. Then, the surface area of the cube can be calculated as follows:
SA = 6 x 4^2 SA = 6 x 16 SA = 96 cm^2
So the surface area of the cube with a side length of 4 cm is 96 cm^2.
How to Find Volume of a Cube?
The volume of a cube is the amount of space inside the cube.
Formula: V = s^3, where s is the length of one side of the cube.
Steps:
- Measure the length of one side of the cube (in any unit of measurement).
- Cube the length of one side (multiply it by itself twice).
- The result is the volume of the cube.
Example:
Suppose the length of one side of the cube is 4 cm. Then, the volume of the cube can be calculated as follows:
V = 4^3 V = 64 cm^3
So the volume of the cube with a side length of 4 cm is 64 cm^3.
That’s it! With these simple steps, you can easily calculate the surface area and volume of a cube.
Hope you liked the Cube volume and surface area calculator .Have you tested horizontal tank volume calculator? Also sphere surface are calculator.